Today we finish finish Section 3.6 and start Section 3.7. Read Section 3.7 (just Markov chains part). Work through suggested exercises.
The midterm is on Saturday, November 9, 2-4pm. It will cover until the end of Section 3.5. Old midterms are on OWL. Room assignments are on OWL and were announced.
Midterm Review sessions: Nov 6 and 7, 4:30-5:30pm, UCC146. Bring questions.
Also extra help sessions announced on OWL.
Also, I'll probably have time in class on Friday to take questions.
Math Help Centre: M-F 12:30-5:30 in PAB48/49 and online 6pm-8pm.
My next office hour is Friday 2:30-3:20 in MC130.
No homework this week.
Any rule $T$ that assigns to each $\vx$ in $\R^n$ a vector $T(\vx)$ in $\R^m$ is called a transformation from $\R^n$ to $\R^m$ and is written $T : \R^n \to \R^m$.
Definition: A transformation $T : \R^n \to \R^m$ is called a
linear transformation if:
1. $T(\vu + \vv) = T(\vu) + T(\vv)$ for all $\vu$ and $\vv$ in $\R^n$, and
2. $T(c \vu) = c \, T(\vu)$ for all $\vu$ in $\R^n$ and all scalars $c$.
Note: If $T : \R^n \to \R^m$ is a linear transformation, then $T(\vec 0) = \vec 0$. (Take $c = 0$ in 2.)
Theorem 3.30: Let $A$ be an $m \times n$ matrix. Then $T_A : \R^n \to \R^m$ is a linear transformation.
Theorem 3.31: Let $T : \R^n \to \R^m$ be a linear transformation. Then $T = T_A$, where $$ A = [\, T(\ve_1) \mid T(\ve_2) \mid \cdots \mid T(\ve_n) \,] $$
The matrix $A$ is called the standard matrix of $T$ and is written $[T]$.
Example 3.58: Let $R_\theta : \R^2 \to \R^2$ be rotation by an angle $\theta$ counterclockwise about the origin. Show that $R_\theta$ is linear and find its standard matrix.
Solution: We need to show that $$ \kern-8ex R_\theta(\vu + \vv) = R_\theta(\vu) + R_\theta(\vv) \qtext{and} R_\theta(c \vu) = c \, R_\theta(\vu) $$ A geometric argument shows that $R_\theta$ is linear. On board.
To find the standard matrix, we note that $$ \kern-8ex R_\theta \left( \coll 1 0 \right) = \coll {\cos \theta} {\sin \theta} \qqtext{and} R_\theta \left( \coll 0 1 \right) = \coll {-\sin \theta} {\cos \theta} $$ Therefore, the standard matrix of $R_\theta$ is $\bmat{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \emat$.
Now that we know the matrix, we can compute rotations of arbitrary vectors. For example, to rotate the point $(2, -1)$ by $60^\circ$: $$ \kern-7ex \begin{aligned} R_{60} \left( \coll 2 {-1} \right) \ &= \bmat{rr} \cos 60^\circ & -\sin 60^\circ \\ \sin 60^\circ & \cos 60^\circ \emat \coll 2 {-1} \\ &= \bmat{rr} 1/2 & -\sqrt{3}/2 \\ \sqrt{3}/2 & 1/2 \emat \coll 2 {-1} = \coll {(2+\sqrt{3})/2} {(2 \sqrt{3}-1)/2} \end{aligned} $$
Rotations will be one of our main examples.
The applet gives examples involving rotations.

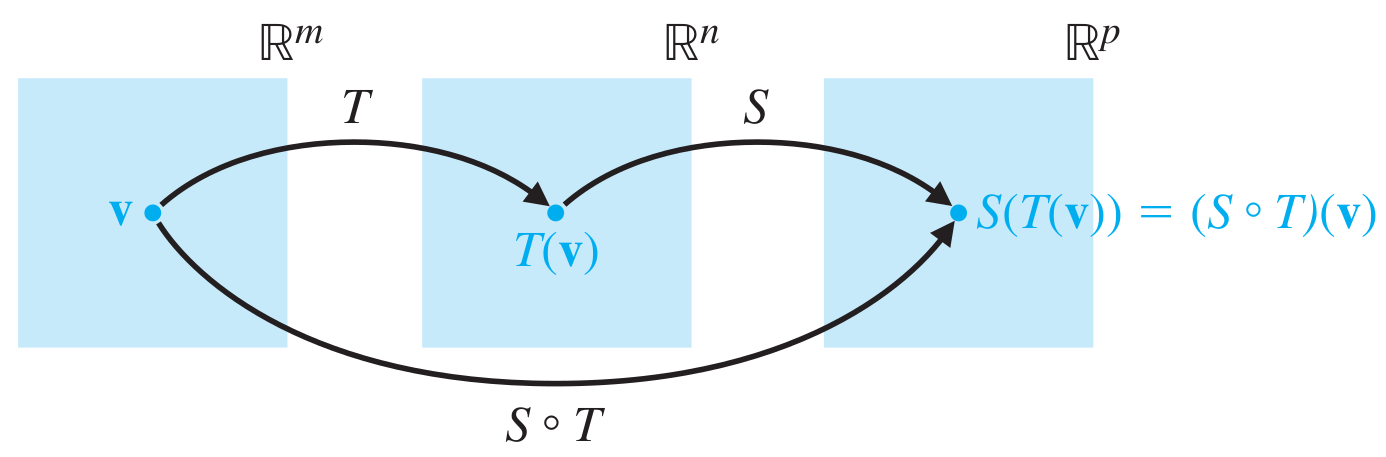
Any guesses for how the the matrix for $S \circ T$ is related to the matrices for $S$ and $T$?
Theorem 3.32: $[S \circ T] = [S][T]$, where $[\ \ ]$ is used to denote the matrix of a linear transformation.
Proof: Let $A = [S]$ and $B = [T]$. Then $$ \kern-6ex (S \circ T)(\vx) = S(T(\vx)) = S(B\vx) = A(B\vx) = (AB)\vx $$ so $[S \circ T] = AB$. $\qquad\Box$
It's because of this that matrix multiplication is defined how it is! Notice also that the condition on the sizes of matrices in a product matches the requirement that $S$ and $T$ be composable.
Example 3.61: Find the standard matrix of the transformation that rotates $90^\circ$ counterclockwise and then reflects in the $x$-axis. How do $F \circ R_{90}$ and $R_{90} \circ F$ compare? On board.
Example: It is geometrically clear that $R_{\theta+\phi} = R_\theta \circ R_\phi.$ This tells us that $$ \kern-9ex \bmat{rr} \cos(\theta+\phi) & \!-\sin(\theta+\phi) \\ \sin(\theta+\phi) & \cos(\theta+\phi) \emat = \bmat{rr} \cos(\theta) & \!-\sin(\theta) \\ \sin(\theta) & \cos(\theta) \emat \bmat{rr} \cos(\phi) & \!-\sin(\phi) \\ \sin(\phi) & \cos(\phi) \emat $$ This implies some trigonometric identities. For example, looking at the top-left entry, we find that $$ \cos(\theta+\phi) = \cos(\theta) \cos(\phi) - \sin(\theta) \sin(\phi) $$ Other trig identities also follow.
Note that $R_0$ is rotation by zero degrees, so $R_0(\vx) = \vx$. We say that $R_0$ is the identity transformation, which we write $I : \R^2 \to \R^2$. Similarly, $R_{360} = I$.
Since $R_{120} \circ R_{120} \circ R_{120} = R_{360} = I$, we must have $[R_{120}]^3 = [I] = I$. This is how I came up with the answer $[R_{120}] = \bmat{rr} -1/2 & -\sqrt{3}/2 \\ \sqrt{3}/2 & -1/2 \emat$ to the challenge problem in Lecture 15.
Our new point of view about matrix multiplication gives us a geometrical way to understand it!
Definition: Let $S$ and $T$ be linear transformations from $\R^\red{n}$ to $\R^\red{n}$. Then $S$ and $T$ are inverse transformations if $S \circ T = I$ and $T \circ S = I$. When this is the case, we say that $S$ and $T$ are invertible and are inverses.
The same argument as for matrices shows that an inverse is unique when it exists, so we write $S = T^{-1}$ and $T = S^{-1}$.
Theorem 3.33: Let $T : \R^n \to \R^n$ be a linear transformation. Then $T$ is invertible if and only if $[T]$ is an invertible matrix. In this case, $[T^{-1}] = [T]^{-1}$.
The argument is easy and is essentially what we did for $R_{60}$.
Question 23-1: Is projection onto the $x$-axis invertible? On board.
Question 23-2: Is reflection in the $x$-axis invertible? On board.
Question 23-3: Is translation by a non-zero vector $\vv$ a linear transformation? On board.