 Lines:
$\vn_1$ and $\vn_2$ are vectors that are perpendicular
to the line and not parallel to each other.
$\vd$ is a vector that is parallel to the line.
Lines:
$\vn_1$ and $\vn_2$ are vectors that are perpendicular
to the line and not parallel to each other.
$\vd$ is a vector that is parallel to the line.
These lecture notes https://jdc.math.uwo.ca/l. (That's an "ell" at the end.)
Today we finish Section 1.3. Read Sections 2.0 and 2.1 for next class. Work through suggested exercises.
Homework 2 due Friday at 11:55pm.
Math Help Centre: M-F 12:30-5:30 in PAB48/49 and online 6pm-8pm.
Regular office hours: Mondays, 3:30-4:30, MC130 (Middlesex College) and Fridays, 2:30-3:30 in the Math Help Centre. (But on Monday, Sept 23, I have to change it to 9:30-10:20am.) Drop by with any questions!
If we expand the vector form into components, we get the parametric form of the equations for $\ell$: $$ \begin{aligned} x &= p_1 + t d_1\\ y &= p_2 + t d_2\\ ( z &= p_3 + t d_3 \quad \text{if we are in $\R^3$}) \end{aligned} $$
The normal form of the equation for $\ell$ is $$ \vn \cdot \vx = \vn \cdot \vp , $$ where $\vn$ is a vector that is normal = perpendicular = orthogonal to $\ell$.
If we write this out in components, with $\vn = [a, b]$, we get the general form of the equation for $\ell$: $$ a x + b y = c, $$ where $c = \vn \cdot \vp$. When $b \neq 0$, this can be rewritten as $y = m x + k$, where $m = -a/b$ and $k=c/b$.
Note: All of these simplify when the line goes through the origin, as then you can take $\vp = \vec 0$.
Note: None of these equations is unique, as $\vp$, $\vd$ and $\vn$ can all change. The general form is closest to being unique: it is unique up to an overall scale factor.
 Lines:
$\vn_1$ and $\vn_2$ are vectors that are perpendicular
to the line and not parallel to each other.
$\vd$ is a vector that is parallel to the line.
Lines:
$\vn_1$ and $\vn_2$ are vectors that are perpendicular
to the line and not parallel to each other.
$\vd$ is a vector that is parallel to the line.
Planes: $\vn$ is a vector that is perpendicular to the plane. $\vu$ and $\vv$ are vectors that are parallel to the plane but not parallel to each other.
Both: $\vp$ is the position vector of a chosen point on the line or plane.
It may seem like there are lots of different forms, but really there are two: vector and normal, and these can be expanded into components to give the parametric and general forms.
Example: Find all four forms of the equations for the plane in $\R^3$ which goes through the point $P = (1, 2, 0)$ and has normal vector $\vn = [2, 1, -1]$.
Solution: For $\vp = [1,2,0]$ and $\vn = [2, 1, -1]$, we have $\vn \cdot \vp = 4$. So the normal form is $$ \vn \cdot \vx = 4 .$$ The general form is $$ 2 x + y - z = 4 .$$ To get the vector form, we need two vectors parallel to the plane, so we need two vectors perpendicular to $\vn$. Can get these by trial and error, for example, $\vu = [-1, 2, 0]$ and $\vv = [0, 1, 1].$ Then the vector form is $$ \vx = \vp + s \vu + t \vv .$$ Expanding into components gives the parametric form: $$ \begin{aligned} x\ &= 1 - s\\ y\ &= 2 + 2 s + t \\ z\ &= \phantom{2 + 2 s + }\, t . \end{aligned} $$ You can also find vectors parallel to the plane by finding two other points $Q$ and $R$ in the plane and then taking $\vu = \vec{PQ}$ and $\vv = \vec{PR}$. If $\vu$ and $\vv$ are parallel, you need to try again.
True/false: The planes given by $$ 2 x + 3 y + 4 z = 7 \qtext{and} 4 x + 6 y + 8 z = 9 $$ are parallel.
If the 9 was changed to 14, the two planes would be equal, but the answer would still be true, as a plane is parallel to itself. The right hand side shifts the position of a plane, but not its orientation.
True/false: The lines given by $$ \begin{aligned} \vx\ &= \vp_1 + t \vd_1, & \vp_1 &= [1,2,3], & \vd_1 &= [2,0,-2] \\ \vx\ &= \vp_2 + t \vd_2, & \vp_2 &= [2,4,6], & \vd_2 &= [2,1,0] \\ \end{aligned} $$ are parallel.
Example 6-1: Find all four forms of the equations for the plane in $\R^3$ which goes through the points $P = (1, 1, 0)$, $Q = (0, 1, 2)$ and $R = (-1, 2, 1)$. Solution on board.
Definition: The cross product of $\vu$ and $\vv$ is the vector $$\vu \times \vv := [ u_2 v_3 - u_3 v_2,\ u_3 v_1 - u_1 v_3,\ u_1 v_2 - u_2 v_1].$$
Theorem 6-2: $\vu \times \vv$ is orthogonal to both $\vu$ and $\vv$. That is, $\vu \cdot ( \vu \times \vv ) = 0$ and $\vv \cdot ( \vu \times \vv ) = 0.$
Explain on board.
Exercise: Try exercise 5 in the cross products exploration. We'll discuss the cross product a bit more later.
Note: The cross product only makes sense in $\R^3$!
Can now finish the previous example, on board.
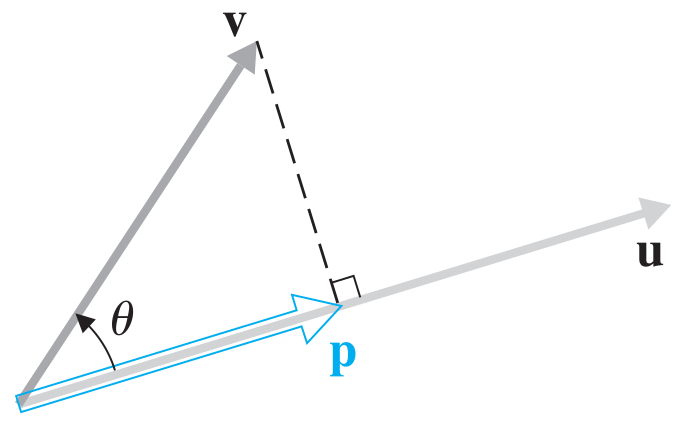 Recall the formula for the projection of $\vv$ onto $\vu$:
$$
\proj_{\vu}(\vv) = \left( \frac{\vu \cdot \vv}{\vu \cdot \vu} \right) \vu .
$$
Recall the formula for the projection of $\vv$ onto $\vu$:
$$
\proj_{\vu}(\vv) = \left( \frac{\vu \cdot \vv}{\vu \cdot \vu} \right) \vu .
$$
Example: Find the distance from the point $B = (1,3,6)$ to the line through $P = (1, 1, 0)$ in the direction $\vd = [0,-1,1]$.
Solution: From the figure we have $d(B, \ell) = \| \vv - \proj_\vd(\vv) \|.$ So we compute $$ \!\!\!\!\!\! \vv = \overrightarrow{PB} = [0, 2, 6] . $$ $$ \begin{align} \!\!\!\!\!\! \proj_\vd(\vv) &= \left( \frac{\vd \cdot \vv}{\vd \cdot \vd} \right) \vd \\[2px] &= \frac{4}{2} [0, -1, 1] = [0, -2, 2]. \end{align} $$ $$ \begin{align} \!\!\!\!\!\! d(B, \ell) &= \| \vv - \proj_\vd(\vv) \| = \| [0, 4, 4] \| \\[2px] &= \sqrt{4^2 + 4^2} = 4 \sqrt{2} . \end{align} $$
Note 6-3: If the line was in $\R^2$ and had been described in normal form, one could instead compute $\| \proj_\vn(\vv) \|$, which saves one step. (Sketch on board if time.)
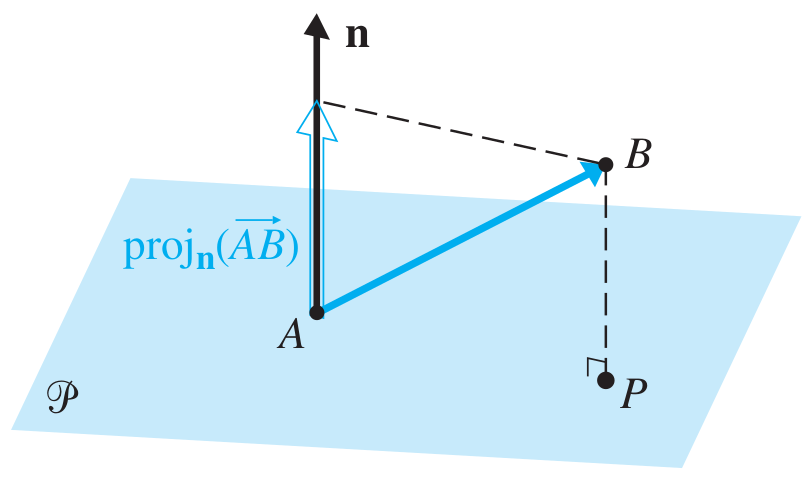 Solution:
The normal vector to the plane is $\vn = [2, 1, -1].$
From the figure, we need to compute
$$ d(B, \mathcal{P}) = \| \proj_\vn(\vv) \| , $$
where $\vv = \overrightarrow{AB}$ for $A$ any point on the plane.
Solution:
The normal vector to the plane is $\vn = [2, 1, -1].$
From the figure, we need to compute
$$ d(B, \mathcal{P}) = \| \proj_\vn(\vv) \| , $$
where $\vv = \overrightarrow{AB}$ for $A$ any point on the plane.
We pick $A = (0, 2, 0)$, so $\vv = [1, 1, 6]$. Then $$ \begin{align} d(B, \mathcal{P}) &= \| \proj_\vn(\vv) \| = \frac{|\vn \cdot \vv|}{\|\vn\|} \\ &= \frac{|-3|}{\sqrt{6}} = 3/\sqrt{6} . \end{align} $$